> DCM Portfolio Optimization > Consideration Set Size

Consideration Set Size

---

If customers do not consider your product, they can’t choose it. There is evidence
that 80% of the uncertainty in choice models can be explained by simply
knowing the consideration set

[ John R. Hauser (1978) ]

Problem

The scope of alternatives recognized as worth of purchase by an individual is usually smaller than the number of available alternatives. It is generally accepted the consideration set at the moment of making the decision is even smaller.

A consideration set is a result of mental selection processes. The most often discussed models are lexicographic, conjunctive, disjunctive, expectancy-value, dominance, ideal point, diffusion and elimination-by-aspects models (see J. Imber and B. Toffler, 2008, Dictionary of Marketing Terms, 4^th Edition, Barron's Business Guides). All the processes consist of a number of product inclusion, comparison and elimination steps done by an individual in their mind prior an actual choice.

Behavioral researchers have examined the process of consideration set formation, and developed various quantitative models. Most of them rely, in some form, on a threshold of alternative acceptance related to a (more or less) universal set of alternatives. However, the views on finding the correct threshold acceptance value are varying.

This communication is an attempt to estimate size of a rationally formed consideration set. The problem of acceptance threshold can be circumvented by switching to information value a consideration set provides to the decision maker.

Information theory basics

The simplest model of quantitative evaluation of an uncertainty is Shannon's information entropy E:

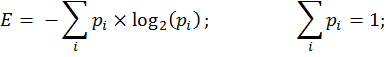
The summation goes over all the states i the system can have, so the sum of the probabilities p_i is equal to 1. 

For example, let's have a system that can have two states (outcomes) "yes" or "no" with the same probability p_yes = 0.5 and p_no = 0.5. The entropy of the system before turning into one of its states is

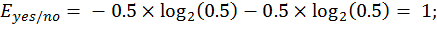
The obtained dimensionless value 1 is the reason for using logarithm with the base 2 by convention as the value can be named as a bit. When the event happens, probability of the resulting outcome (be it "yes" or "no") is 1 and probability of the other outcome is 0 (zero). The entropy of a system that cannot change its state is therefore 0 (zero) bits, i.e. there is no uncertainty. The information obtained from a result of an event is equal to the entropy (uncertainty value) of the state before the event (e.g. purchase) has happened.

Consideration set

The choice probabilities of the alternatives making a consideration set the final decision is made from must be very similar one to another. If any of the probabilities were noticeably lower the respective alternative would have been already excluded from the set. If any of the probabilities were noticeably higher the consideration set would not exist since the respective alternative would be the choice. Therefore, in first approximation, choice probabilities of N alternatives making the set can be taken as equal. Provided the choice will have occurred the choice probability of all alternatives is 1/N. The entropy E_CS of a consideration set before the decision is made is

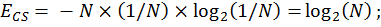
This function is monotonously growing with N and is directly proportional to the inclusive value (IV) of a nested set (for more information please search for 'nested logit inclusive value'). 

In the reasoning that follows the decisions of the kind "should I buy a new car or a fancy holiday on Bahamas" are excluded. It is supposed the consideration set is made of close substitutes, i.e. alternatives from a narrow product category.

A consideration set formation is not without mental cost for an individual. It always takes some effort and time. Because the alternatives are supposed to be from the same category, learning and evaluation of the important aspects of any of them can be taken as equal. Without loss of generality the mental cost per alternative can be set to unity, and the overall mental cost of a consideration set formation is N. The effort devoted to the excluded alternatives is neglected as they are supposed to have deserved much less attention and are virtually forgotten at the time of the actual decision.
A rational consumer, when forming a consideration set, tends to maximize the information value of the set per its total mental cost, i.e. maximize the information I_CS = E_CS/N. Its values for number of alternatives N = 1..7 in consideration set are in the table below.

The highest information value is obtained for 3 alternatives, but the values for 2 and 4 alternatives do not differ much. The reader might recollect size of his or her own consideration set immediately preceding a decision in an actual purchase. The author's one is 3 or 2, or – quite rarely – 4 alternatives when there is an acute desire for a change or diversity. Considering more alternatives is not worth it namely due to rapidly increasing number of required pair-wise comparisons that are not taken in account in this simple model. 2 alternatives require only 1 pair-wise comparison, 3 alternatives require 3 comparisons, and 4 alternatives require 6 of them. It seems to be quite hard to remember more. This factor is in favor of a lesser number of alternatives even in a case the decision maker is familiar with one or more alternatives whose evaluation requires little effort. 

Conclusions

The low number of alternatives predicted in a consideration set of a rational individual might be a surprise to some. However, the range of 2 to 4 acceptable products is typical for calibrated results of brand-price conjoint studies with the total of up to about 35 brands. 5 or 6 alternatives are found for respondents who are more sensitive to price and, therefore, prone to switch among products while 7 or more acceptable alternatives appear to suggest unreliable answers. 

The situation in the real market will not be much different. However, other factors than pure preferences will influence consideration set formation. Immediate accessibility, familiarity, awareness, advertising, display, and other external cues will lead to a situation-specific consideration set being brought to mind of an individual. Such a set should be rather called an evoked set as some authors suggest. A special case, namely at the decision time, is a well formulated recommendation that exceeds the information value of 0.53 bits. It will prevail over the consideration set that might have been built so far independently by the decision maker.

A method for a reasonable cut-off of a number of alternatives in consideration set can be an alternative approach in correction of individual-based preference-share simulations based on a DCM study. Decreasing the number of alternatives for an individual would move the results of simulation closer to the results of first-choice simulation but without the disadvantage of losing the information obtained for the other alternatives. It is known that about 20% or more of obtained information is noise that should be removed. The number of alternatives in a consideration set can be radically decreased by doing so. This idea is the essence of a market share simulator to be developed in the future.