Constant Alternative in Simulation

> Conjoint Method Overview > Constant Alternative in Simulation

Introduction

Choice simulators are most often based on the logit formula that defines the probability of a product choice as a ratio of the odds of the simulated product to the sum of odds of all alternatives in the choice set. Odds are a monotonous function of the utility of the alternative, in DCM modeling usually the exponential of the (McFadden's type) utility. The use of the logit formula is justified if all the alternatives in a simulation are independent. This is required by the assumed multinomial distribution of choice probabilities. However, the estimated "utility" of a constant alternative in a conjoint study, typically the None alternative representing a refusal to choose a product, does not have properties comparable to a product. It should be perceived as a threshold under which a product alternative will not be chosen.

The unsatisfactory results from a simulation where one alternative is a constant alternative can be illustrated by simple thought experiments.

The first thought experiment starts with a single product with a choice probability of 1/2 (0.5) for some customer. This situation can be simulated by two alternatives, one being the product and the other one a None alternative, both having the same utility. Product acceptance is defined this way.

Now we extend the portfolio by adding another product from the category, i.e. a potential substitute, with the same utility for the customer. Common sense tells that the total probability of a choice being made remains 1/2. However, the logit formula gives 1/3 for each of the alternatives, which is the total probability 2/3 for making a choice and 1/3 for not choosing anything. The choice set does not obey the requirement of the IIA - Independence from Irrelevant Alternatives axiom. A remedy would be to multiply odds of the None alternative by 2. When a portfolio is extended to contain N products with the same utilities, the probability of making a choice remains 1/2. To obtain this result from the logit formula, the odds of the constant alternative should be multiplied by N. We can conclude from this experiment, that when a product is added to a portfolio, the utility of the constant alternative utility should be increased.

The two experiments contradict each other with respect to the None alternative. The first experiment is typical for similar and mutually substitutable, that is, correlated products. If a correlated product is added to a portfolio, its addition will not invoke an increase in the total consumption or unit sales. As the current market is typically saturated with the products of the type, the added product cannibalizes on other products. A share simulation is recommended.

The second experiment, rather than for individual products, is more appropriate for alternatives being groups of potential substitutes in a two-level nested multinomial logit model.

Problem

A simulator using the logit formula alone can provide reasonable choice shares for product alternatives both all correlated or all uncorrelated and is widely used for this purpose. However, results from a simulation with a constant alternative may be severely biased. This is caused by neglecting the values of correlation among the products on one hand, and the constant alternative on the other.

The problem can be solved by applying some of the models not requiring IIA, namely Nested Multinomial Logit or GEV - Generalized Extreme Value models. The nested model is sometimes called sequential. Unfortunately, the use of these models in market research practice is hardly feasible. The estimated structural parameters (dissimilarity indexes) and the estimated utilities in the nests related to them are heavily confounded. A comparison of estimated utilities from different nests is therefore unreliable. In addition, the software is expensive, its usage complicated, and requires a specialist in the field. Considering the current revenues for an average study, the involved labor would not pay back. A simpler solution is desirable.

Solution

In the market research practice, the most common objects of conjoint analysis are products from a narrow category. In such a case, all the products can be understood as correlated (substitutes) and can create a single nest. The None alternative can be another nest uncorrelated with any of the products. However, these assumptions do not remove the requirement to use full-fledged analysis and simulation tools.

The order of the steps is hierarchical for modeling reasons. They may proceed in any order in the mind of a decision-maker. The structure of the model for I correlated items is in the picture below.

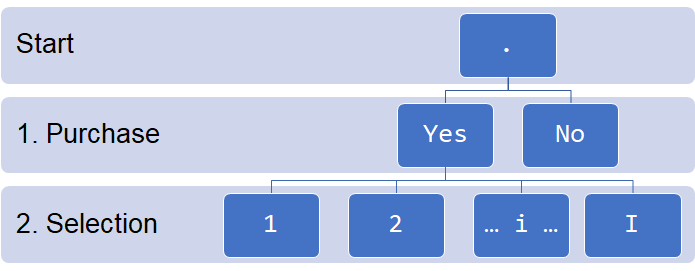
The first level of the nested structure handles a customer's decision to purchase anything with probability

where Ε_portf is Von Neumann-Morgenstern's utility of the product portfolio and V_none is utility equivalent to no purchase. Probability of no choice is a complement to the probability of the purchase equal to 1 - P_purchase.

The second level of the nested structure handles the selection of the product to be purchased. A probability of selection of the i-th product in the nest of perfectly correlated products is the logit formula

where V_{prod_i} is the utility of i-th product. This probability is also used for the computation of Von Neumann-Morgenstern's utility Ε_prod of the product portfolio used in equation (1).

The joint probability P_{choice_i} of the whole process of choosing an item i is the product of probabilities of both steps.

The four equations above allow for the construction of a choice simulator respecting the meaning of the None constant alternative as obtained from a common CBC exercise without requiring to estimate structural parameters of dissimilarity.

The order of the steps in the nested structure is purely formal. In reality, a customer will first overlook available products, then select the most appropriate one, and only then decide if it is worth of purchase. We can, therefore, ask if the theoretical Von Neumann-Morgenstern's utility, which is the probability-weighted sum of mean utilities of the alternatives, might be replaced by the utility of the best product in the product portfolio.

In the picture below is a portfolio composed of two items, one with the fixed utility equal to 2.0 and the other with utility changing from -3.0 to 4.0 logit on the horizontal axis.

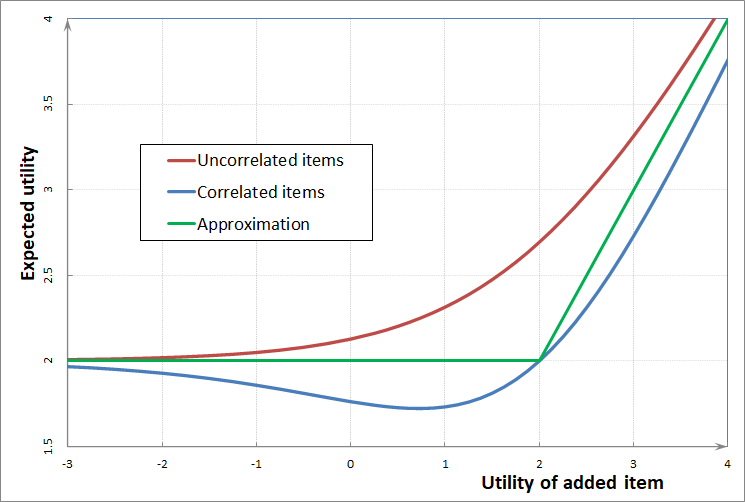
The expected utility of the portfolio of perfectly correlated items (product substitutes) is shown as the blue line. It can be approximated by the highest value of the two utilities.

The approximation (5) replaces equation (3) and is depicted as the two green straight line segments in the picture.

The expected utility of the portfolio of completely uncorrelated items (product complements) is computed as a logarithm of the sum of odds and is known as IV - inclusive value or log-sum value. Inclusive value is always higher than the approximate value. With a growing number of items in a portfolio, a relative difference of the approximation from the Von Neumann-Morgenstern's utility decreases because the inclusive value of a portfolio always grows with adding an item while neither the Von Neumann-Morgenstern's utility nor its approximate value can exceed the maximal utility value in the portfolio.

As aside

The fact the Von Neumann-Morgenstern's utility violates a basic axiom of choice theory may serve as a support to the approximation (5). Implied by the theory, adding an alternative to a nest cannot lower the desirability of that nest. (Cited from berkeley.edu source).

With regard to the presumed customer's behavior, basic axioms of choice theory, and a systematic error of the approximation far below the usual errors of utility estimates, we have adopted the maximum item utility as an approximation of a portfolio utility into our choice simulators. Its application is much simpler than that of the theoretical Von Neumann-Morgenstern's utility. In a summary, choice probabilities of items in a simulation are computed from the acceptance of the best product partitioned by odds of all products in the portfolio. This approach was already suggested by McFadden (1974) as the "maximum logit" model. As far as we know, it has not been applied to a choice simulator provided by other sources.

Addendum

Some time ago we have abandoned the traditional "None" constant alternative in CBC exercises and replaced it with an additional "calibration" question on the stated purchase intention conditional to the chosen item. This approach has allowed for re-scaling of the raw utilities obtained from the hierarchical-Bayes estimation, setting the individual acceptability thresholds and use of a non-compensatory model of expected market potential estimation. This was facilitated by implementing the described two-level nested model of choice.

In a quick view it would seem very easy to create more uncorrelated nests each with correlated products, and apply the described approach. A very limited number of attempts revealed this is not a generally useful approach. Such nest might be very rarely found in market research practice.

References

McFadden, D. (1974). "Conditional logit analysis of qualitative choice behavior." In Frontiers in Econometrics, ed. P. Zerembka, 105–142. New York: Academic Press, 1974.

Abstract

Introduction

Problem

Solution

Addendum

References