 > CSDCA - Common Scale
Discrete Choice Analysis > Relaxed Non-compensatory Simulation
> CSDCA - Common Scale
Discrete Choice Analysis > Relaxed Non-compensatory Simulation  > CSDCA - Common Scale
Discrete Choice Analysis > Relaxed Non-compensatory Simulation
> CSDCA - Common Scale
Discrete Choice Analysis > Relaxed Non-compensatory Simulation
Test everything. Hold on to what is good.
1 Thessalonians 5:21
Abstract
A relaxed non-compensatory model of product choice probability is presented. The model is non-compensatory in the regions where any attribute takes a value under its threshold and the product is assigned zero choice probability. In the regions with all attributes set above their threshold values, the model is additive and, therefore, compensatory. Mathematical formulation is analogous to Stone-Geary utility of a consumption bundle. The model has been developed for simulation of choices that do not require high involvement and a decision maker is supposed to optimize their choices.
The fully non-compensatory model of choice has been developed for situations when making a decision requires high involvement, the decision may be postponed (up to indefinitely), and the choice may be restricted by some endogenous or exogenous barriers. Much more frequent are everyday decisions that require only low involvement, are made quickly or even hastily, and choice optimization is superficial. Such decisions are made mostly on inner convictions and subjective perceptions that cause implicit rejection of some products, be it due to presence of some unacceptable or absence of some required aspects. In terms of conjoint terminology, an attribute may have a threshold level under which a product becomes unacceptable. At the same time, the decision maker will regard and appreciate the total sum of benefits exceeding the thresholds rather than to optimize the choice so that all important aspects of a product are satisfied more or less equally. This corresponds to an additive model of utility. By allowing part-worths to be additive the non-compensatory feature of the model can be relaxed.
When a product is understood as a bundle of its aspects the standard compensatory model can be formally related to and compared with the Cobb-Douglas utility function.
In the fully non-compensatory model, a perceptance of a product is [non-linearly] proportional to product of perceptances of the product aspects. We can partially resign on the non-compensatory property of the model and omit denominator in the perceptance definition formula. For a product with K aspects we obtain the total product odds,
| Product_odds | = (Odds(aspect_1) – Odds(threshold_1))β1 × (Odds(aspect_2) – Odds(threshold_2))β2 × ( ... ) × (Odds(aspect_K) – Odds(threshold_K))βK |
where βk is a weight related to k-th attribute. This equations can be compared with the Stone-Geary utility function for preference odds of a consumption bundle.
| Bundle_odds | ≘ (Quantity(product_1) – Subsistence(product_1))Importance_1 × (Quantity(product_2) – Subsistence(product_2))Importance_2 × ( ... )... × (Quantity(product_K) – Subsistence(product_K))Importance_K |
 As
aside
As
aside
Consumption that exceeds the subsistence level creates the well being, i.e. the utility function. Quantities of consumed products are proportions summing to 1, and are proportional to probabilities of their choice. When a single product is understood as a bundle of aspects, the same view can adopted. When a quantity above subsistence raised by its importance is related to odds of an aspect, the term becomes odds of an aspect in a way similar to the standard additive and compensatory model. Odds of a threshold can be related to a "subsistence" level, i.e. a level that must be surpassed so that the aspect has positive (part-worth related) odds.
The relaxed non-compensatory model of choice assumes the probability of a product to be chosen is zero if part-worth of any aspect of the product is less or equal to part-worth of the threshold. The product will not be consumed by the individual. This is with agreement with all non-compensatory models of choice and reflects the most common behavior on the market.
 As
aside
As
aside
 As
aside
As
asideThe estimated part-worths are transformed to odds and choice is simulated using Luce theorem (i.e. logit formula as if random utilities of McFadden-type were used).
 As
aside
As
aside
The model was applied on a set of 20 snacks offered by a single vendor of fast food. The snack market prices ranged from 39 to 129 Kč (CZK). The products were divided into 4 groups, namely the big (10 products), special (4 products), fit (2 products) and small ones (4 products) groups.
For each group, the preferential order was obtained in the PRIORS section of the questionnaire. Prior estimates of just unacceptable prices were determined for groups of big and special products with the Gabor-Granger method using randomly chosen prices. The higher value of the two was used as the prior value for threshold estimation.
The CBC section consisted of 10 choice tasks, each with 7 snack profiles and the constant alternative "None". Products were tested on 5 price levels, with 1 level under and 3 levels above the market price. The prices were selected from a vector of 21 values generated so that each product was tested in the range from about 96% to 119% of the market price.
The web questionnaire was created in Sawtooth SSI ver. 8.4.8 system. Data was processed using Sawtooth CBC/HB 5.5.4 and IBM SPSS Rel. 23 software. The simulator was written in MS Excel 2007.
 As
aside
As
aside
The centered raw part-worths of aspects as obtained directly from the analysis by HB - Hierarchical Bayes
estimation are shown in the leftmost picture below. Perceptances computed from them
respecting the attribute thresholds are in the middle picture. They can be compared with one another. Influences
computed from non-negative perceptances and re-scaled so that their sum is 100%, are in the rightmost picture
below.
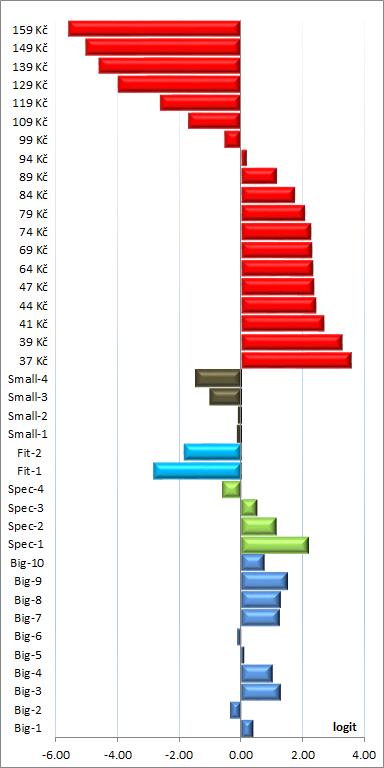
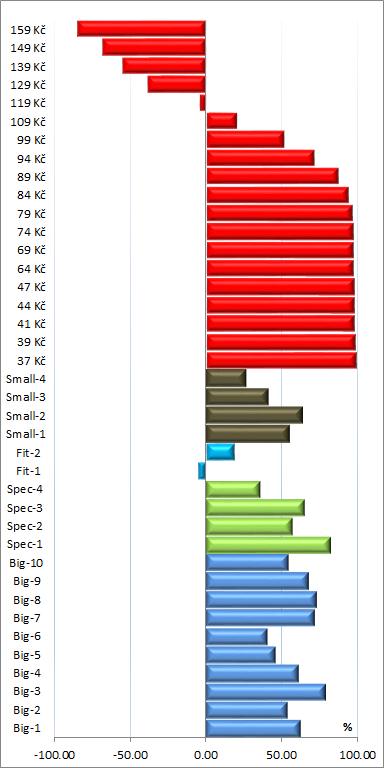

The raw part-worths with the zero value defined as the mean of attribute level part-woths are incomparable between attributes, and are sufficiently informative only for an experienced analyst. Perceptances, in contrast, have the common zero value at the thresholds, and allow for additional conclusions.
First, perception of a price to be too high for a snack starts with a price around 119 Kč or higher, and not at 99 Kč as might be expected. Such observations have been observed previously and suggest the positive effect of the "last dollar" of a round value is not always the case. In our experience, an apparent elasticity increase often starts at about 10% above the round value. Second, consumers expect to spend 80 Kč or more for a snack. A lower price is not perceived as a bonus if the product is adequate for the price. As for the product portfolio, the Fit-1 snack is a failure. The both "healthy" Fit products have low acceptance and, in our view, do not fit the portfolio composed of more or less "unhealthy" products.
The influences in the rightmost picture provide information that could be derived from a sequence of simulations. The increase of purchase willingness for the lowest prices is due to the fact that the products were offered in the competitive CBC environment where an identical product is offered for various prices thus artificially increasing the elasticity. A noticeable observation is that the product Big-4 has its influence comparable to even the lowest tested price. It is virtually the pilot product for a snack provider presentation as it is influencing most customers (the distribution is not shown here).
The choice simulations using three models of choice, namely the standard (compensatory) model, relaxed (non-compensatory) model and prospect (non-compensatory) model, for the current retail prices, are shown in the picture below.
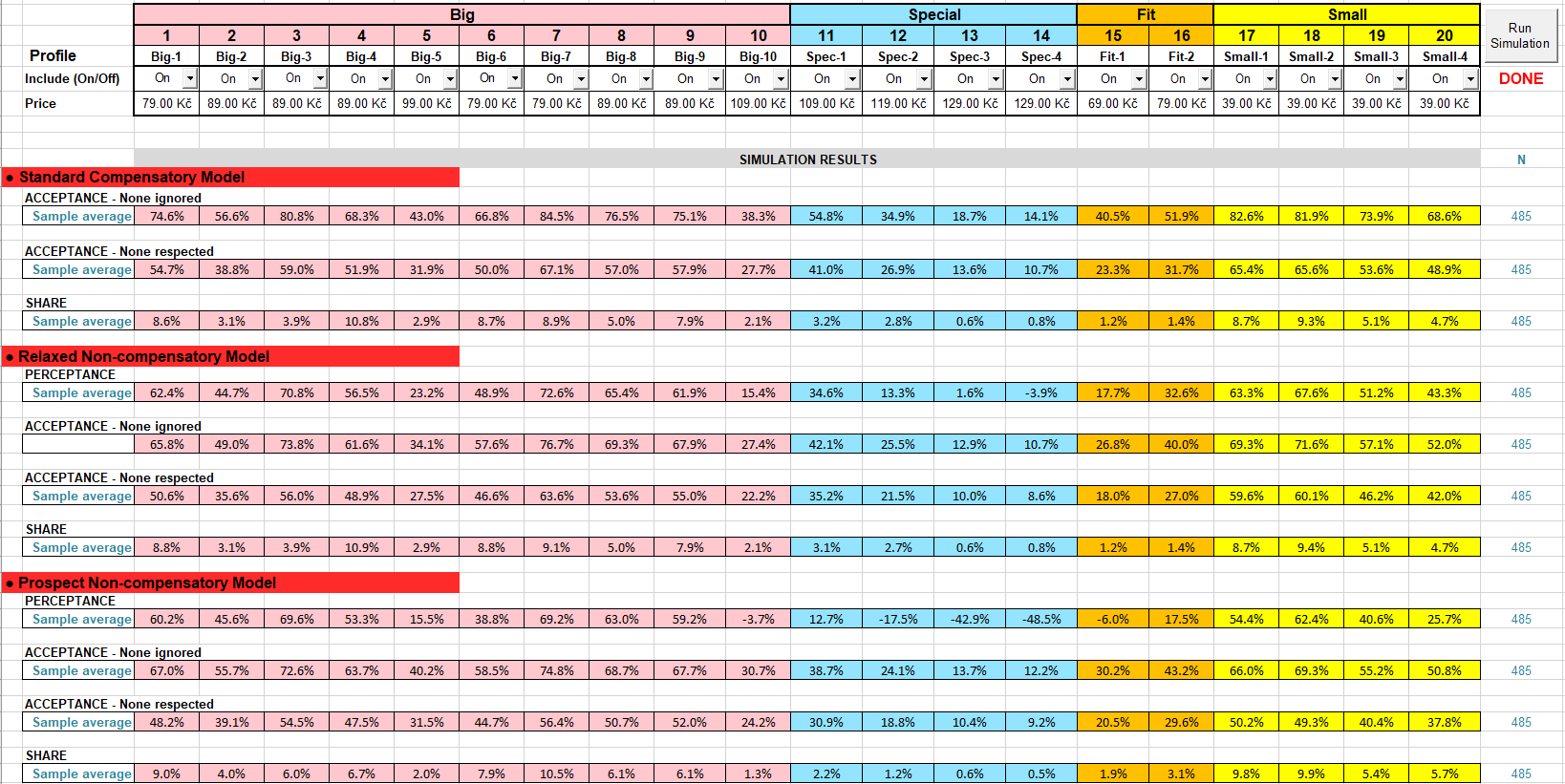
Static characteristics for profiles, i.e. acceptances and perceptances, differ because of different formulas for computing product utilities. Acceptances estimated for the standard compensatory model are generally higher than for non-compensatory models. Strictly speaking, perceptances are defined only for non-compensatory prospect model. They are generally lower than those approximated for the relaxed model. Some perceptances in the group of special snacks are negative due to their prices that seem too high for many consumers. The discrimination power of the prospect model is apparently higher than for the relaxed model.
The estimated shares for the standard and relaxed models are nearly identical. This supports the assumption that the items selected in CBC were sufficiently above the unacceptability thresholds. On the other hand, shares estimated from the prospect model are noticeably lower for more expensive snacks. The reason may lay in the model itself. The prospect model was designed for products that require deep reasoning about all aspects of a single product before the actual choice proceeds. Therefore, if there are only two aspects, the price may take over and be critical. In consumer products such as snacks this may not be the case.
An important outcome of a brand-price study is price sensitivity. Text-books of microeconomics often show a linear dependence of demand on price. Such a relationship neither has a theoretical background nor is actually observed. Neo-classical theories based on budget restraints lead to close-to-linear log-log dependencies with different coefficients of proportionality for different products. Unfortunately, this approach is unusable in analysis of CBC data with a limited number of choices. The approach used by us is independent from any theory. It is based on the assumption that the (isolated) willingness to pay a given amount of money for a product from a category is constant. The choice probability depends both on this willingness and felicity of the product. Individual prices corresponding to the levels of CBC price attribute are selected from a fixed, approximately geometric, sequence of values so that each product has its own sub-class of prices. Part-worth for each individual price shown in the study is estimated independently from each other.
An often met property in choice simulations is an unrealistic, too low switch from expensive to cheaper products when prices of all products are increased by the same percentage. The switch is nearly null if price part-worths are close to linearly dependent on logarithm of prices which is often the case. It is believed the introduction of price thresholds might correct this behavior as the thresholds might function similar to the unknown budget constraints. The predicted shares for the four groups of snacks at the market prices and all prices increased by 19% are shown in the table below.
| Snack group | Standard model | Relaxed model | Prospect model | |||
|---|---|---|---|---|---|---|
| Market price | Dtto + 19% | Market price | Dtto + 19% | Market price | Dtto + 19% | |
| Big | 62.0% | 49.7% | 62.4% | 47.0% | 59.5% | 36.4% |
| Special | 7.4% | 3.3% | 7.1% | 2.5% | 4.6% | 1.3% |
| Fit | 2.7% | 2.9% | 2.6% | 2.9% | 5.0% | 5.6% |
| Small | 27.9% | 44.1% | 27.9% | 47.6% | 30.9% | 56.7% |
The standard compensatory model predicts a moderate increase of cheaper products on account of expensive ones. This is due to noticeably lower elasticity in the range of lower prices compared to higher ones. The switch predicted by the relaxed model is perceptibly, but not dramatically, higher. A quite pronounced switch is predicted by the prospect model. Unfortunately, no market data exist to determine which of the models might be closer to reality.
The reader may duplicate the shown results using the simulator available for download. The basic properties and usage control of the simulator are described on the page DCM Excel Choice Simulator (under preparation).
 As
aside
As
aside
The results suggest the relaxed non-compensatory model is suitable for situations where choice decision takes place immediately in the presence of products that are more or less substitutes. The results do not differ much from the standard compensatory model in the range of product aspects commonly found on the market. This concerns FMCG/CPG products in stores with a rich selection, consumer goods in catalogs of online stores, and the like. However, when less known or more complicated products are tested, it is believed the CSDCA methodology can give an in-time notice of some problems thanks to possibility to compute perceptances of the aspects for which thresholds have been determined. This is on account of questionnaire and data processing simplicity. The relaxed non-compensatory model can be viewed as a compromise between the standard compensatory and prospect non-compensatory models.