 > Conjoint
Method Overview > Attribute Properties and Models
> Conjoint
Method Overview > Attribute Properties and Models
Conjoint analysts and discrete choice empiricists have always faced the trade off between model complexity and ease of model estimation known as "curse of dimensionality". As the number of dimensions increases, an exponential increase in sample size is needed to maintain reliable model estimation.
[ McFadden, D. (1974), Conditional Logit Analysis of Qualitative Choice Behavior. New York Academic Press, 1974. ]
The foundation of the conjoint model is the additive part-worth kernel. In short, indirect utility of a product is built as sum of attribute level part-worths and, possibly, interaction terms between attribute levels. The part-worth is an additive contribution to the utility.The standard conjoint attribute is represented by discrete values, called levels, of a standard measurement variable. It is assumed that attributes are separable, i.e. any level of an attribute can be set independently from levels of all other attributes at least in a certain range.
| In respect to attribute properties, reliability of estimated level part-worths is decreased in the following cases. |
|
Unfortunately, no universal solution exists. Every aspect must be considered separately and a compromise be searched for.
Part-worth of a level is an interval scaled measure of the level preference relative to other levels. Usually, its zero value is either assigned to one of the levels of the attribute (dummy coding), or the part-worths of all levels are shifted so that their mean is equal to zero (effect coding). In the former case, when the reference level is changed, or in the latter case, when a level is added to or removed from an attribute, values of all level part-worths change.
A comparison of the part-worths can be done only within the attribute. Comparing part-worths of different attributes is meaningless due to the scaling of part-worths with an arbitrary reference point for each attribute. This is the direct consequence of the conjoint model definition. However, differences between part-worths of one attribute can be compared with differences of part-worths of another attribute. This is the main property all what-if simulations are based on.
 As aside
As aside
In contrast, elasticity of substitution (see below) for attributes of ratio scaled variables can be mutually compared.
 As aside
As aside
Preferences of levels of a nominal attribute have no natural order. Brand, flavor, shape, color, presence or absence of some feature (in products, packages or bundles) and other characteristics have unforeseeable preferences.
Levels of a nominal attribute must be defined so that close substitutes are avoided. Whatever small is the difference between two levels, humans perceive them as different when shown side by side. Their presence leads to an artificially increased importance of the attribute.
Preferences of ordinal attribute levels have a natural order but the model of their numerical values is unknown. Examples may be a length of obligation, warranty period, quality expressed in non-quantitative units (e.g. low, medium, high; class I, II, III). Price often belongs to this group when the range is too broad or includes the zero value (a free service component, bonus, sample, coupon or other motivator). A general recommendation is to use levels at intervals a priori equidistant in their effects. Level part-worths of an ordinal attribute can be constrained and reliability of their estimates increased. However, this is not a rule. E.g., a bigger, stronger and faster car, keeping all other properties equal, is not better if one has no place to keep it in, or has an 18-year old son with a fresh driving license eager to show off his endowment to drive fast.
There is rarely a need to define more than five levels of a clearly ordered attribute as most simulators allow for an interpolation between the levels. Too many levels significantly lower the precision of the part-worth estimates simply because of the need to estimate too many parameters.
To define and treat level part-worths of a quantitative attribute, the following considerations are useful.
These steps can often help in the parameter estimation problem. Their application is limited to monotonous and, in some special cases, mono-modal dependencies. Constraints should always be applied with caution. While a lower price (in a conjoint study) never means a lower indirect utility this may not be the case for a benefit. Saturation of a need and/or expectation is often reached at some level. A too high benefit value that cannot be fully utilized may lead to discontentment of the respondent and refusal of the profile despite an affordable price. Such local extremes are rare but cannot be excluded.
Econometric, psychometric and biometric sciences offer functional models of human behavior and perception. The models can adequately describe human behavior such as reactions to delighters or must-haves in the frame of precision achievable in MR. In a hyperbolic statement, the way of understanding the "value" or "utility" can be regarded as the human sixth sense governed by the universal laws of the nature.
| The following behavioral models of monotonous nonlinear influences can be used: |
|
If a quantitative attribute is uncorrelated with other attributes, the whole set of part-worths related to the attribute can be replaced by a conjoint kernel constituent that is a function of the quantitative variable representing the attribute. The part-worth functions can be used in modeling refusal due to price, saturation of needs, or insensitivity to benefits or detriments in certain value regions, etc.
For example, when satisfaction is expected to grow with the value of a quantitative benefit it is often observed that the dependence of the satisfaction part-worth on the benefit is sigmoid, i.e. has both convex and concave regions with an inflection point in between. It has the shape of a delighter in its left (low values) part, then changes into the shape of a must-have and finally shows off saturation.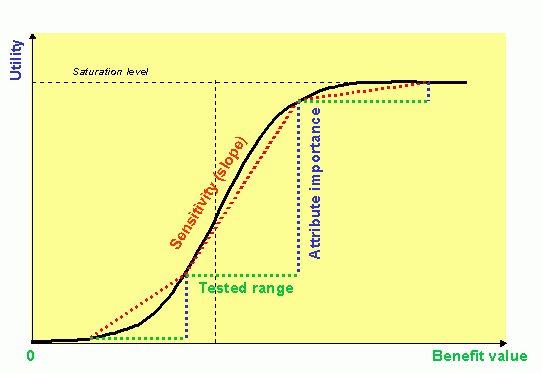
This form of dependence can be formally obtained by introducing Stevens power law into Michaelis-Menten biometric model for influence saturation. The steepness of the curve reflects sensitivity (i.e. elasticity) at the respective value of the benefit. As the location, shape and range of the curve strongly differ among individuals, the elasticity values based on a broad interval of the attribute values may be misleading. Elasticity at the inflection point of the curve is clearly much higher than that computed as an average for the whole interval of values. Experimental elasticity of substitution is always dependent on the range of values it is based on.
 As aside
As aside
The simplest model for dependence of a quantitative attribute on its value is partial derivation (slope) of the part-worth by logarithm of the attribute value. If the underlying model of utility is CES - Constant Elasticity of Substitution or CDES - Constant Difference Elasticity of Substitution constrained by a fixed budget, and the attribute is gross price of the product, it is related to common price elasticity. Provided the additive kernel (compositional model) of conjoint is valid, the derivation of the related part-worth by logarithm of the attribute value is equivalent to partial elasticity coefficient of substitution. Its value can be often viewed as constant in a reasonably broad interval of values.
The stated elasticities of substitution can be of a great help for an informed user. They may be understood as normalized attribute importances. If the same model can be applied to all quantitative attributes and the calculated elasticity coefficients be recognized as constant there is a possibility to compare attributes independently from the tested range of their values. This is of an indisputable advantage compared to the standard attribute importances. The approach can be used for price-based and quantitative benefit or detriment attributes based on ratio scaled variables varied in sufficiently narrow ranges above the zero values. If the regions are wider or close to the zero, the elasticities may differ for different regions (cf. the picture for a benefit utility above).
In practice, functional analysis and modeling of conjoint attributes is done only rarely. Often we cannot tell for sure between concave, linear or convex dependence. A generally safe, but less informative way, is to stick to discrete level part-worth along with acceptance-based measures of estimated utilities as described in the chapter on utility Interpretation. This requires to include rating questions in the questionnaire and apply calibration of the utilities with the disadvantage of a longer interview. A behavior-based segmentation such as LCA - Latent Class Analysis may be helpful to avoid mixing customers with different types of perceptions.
 As aside
As aside
Basically, all the rules for a quantitative attribute are in effect, but some additional aspects must be regarded.
The function of price in a conjoint study substantially differs from that on the market. A higher market price is often an indicator of one or more benefits such as image, quality, range of services, post-purchase service availability, customer relationship etc. In a conjoint exercise, price is varied within some interval independently of the product quality or performance. Respondents recognize this in a short time and move their attention from other attributes to the price.
Another important aspect is price awareness. While it is quite high for CPG/FMCG goods and many durables, users often have only a vague idea of how much they actually pay for some banking, telecommunication, utility and other not quite frequently considered services. Said very politely, distorted statements in this respect are not exceptional.
Using a price tag apparently above the market one makes a respondent to ignore the profile and select a product with a more favorable price, or nothing. A remedy is to use a higher number of choice sets in the exercise. In a branded of class-based study, too high price shown early in the exercise may evoke a perception of an (overly) expensive brand or class of products, and lead to higher refusal of the brand or class on next choice screens.
A markedly more detrimental effect have excessively low prices. Once a respondent has seen a product at a very attractive price, their tendency to refuse products at quite common prices is increased. This leads to a higher number of escape choices (selecting "none") and loss of information obtained form the exercise.
A general recommendation is to set price values around the market ones so that the general notion of the tested products pricing is not distorted. The interval should be as narrow as only possible just to guarantee a reliable determination of the price sensitivity.
As the product utility is generally computed by summing attribute part-worths the common requirement is to obtain all part-worths with about the same accuracy and precision. To achieve this, all attributes should have the same number of levels given the null hypothesis that all attributes have the same relative importance. Such a condition can hardly be met in practice. The number of levels, span and spacing must respect the set of studied products and reflect the real world conditions.
It is well known that the sensitivity to attribute levels grows with their number. This effect is believed to have psychological reasons, probably due to an excessive attention to a higher number of different values compared to those of other attributes.
The number of levels of a nominal or ordinal attribute usually comes from the essence of the studied problem. A researcher has usually only little room to influence it, but in respect to reliability of the estimates, a lower number is often better.
The number of levels of a quantitative attribute is given namely by the requirements of the level spacings (see below). It is useful to partition the investigated products into product classes such that the problematic attribute is varied in each class over the same number of levels. This number should be kept as low as possible. The total number of levels of an attribute is that of the overlay of the levels assigned to product classes the conjoint exercise is composed off.
Numerical models of choice behavior have been derived on the assumption that the number of observations is infinite. In reality, the finite number of choices leads to partial leveling of the estimated differences between level part-worths within an attribute of any type.
To explain this problem we can imagine a CBC - Choice Based Conjoint exercise for a set of products A, B, C, ..., Z that are labeled in the order of decreasing preferences for a person. Say the products A and B make the consideration set with product A strictly preferred over B. Choice tasks are constructed as orthogonal, i.e. every pairwise combination of products appears in all tasks equally often. If none of the products A or B is present in the CBC task and some is chosen, it is with low involvement and more or less by random because something must be chosen. This may correspond to a situation when none of the favored products is available and the household must be replenished. If just one of the products A or B is present then it is chosen. If both products A and B are present, A is chosen. Products C, D, ..., Z will get low utility values close one to another due to the randomness. Products A and B will get high utilities with utility of B only slightly lower. This is because product A together with B will be presented in the choice sets much less often than either the A or B with any other products. E.g. with the total of 26 products shown by 4 in a choice set, the ratio is 3(A+B) : 22(A+not_B) : 22(B+not_A). The higher the total number of tested products and lower the number of products shown in a choice set, the more pronounced this effect will be.
The above effect is noticeable for the dominating attribute at its first and second best level. A formulation of product classes based on the preferred levels with the other attributes set to compensate for the preferences usually helps. The problematic levels are then shown more often side by side than it is in the strictly orthogonal design.
The leveling effect is often observed for levels of quantitative attributes. Perception of the levels is in a great deal influenced by the fact that the level values are different. In case of a "linear" dependence, estimated differences between effects of level values 1.1, 1.2, 1.3 and 1.4 will tend to be nearly the same. If the value 1.3 is omitted, differences between 1.1, 1.2 and 1.4 will tend to get closer to each other. It is suggested that levels of quantitative attributes should be spaced so that the effect (rather than value) differences between consecutive levels are approximately equidistant. If the behavioral or econometric model of the attribute is known or assumed the spacing of level values should be based on it.
The differences between estimated part-worths of attribute levels, i.e. sensitivities to the stimuli, depend on many factors, namely on the range and number of levels. The broader the range and lower the number of levels the lesser the sensitivity per a unit of the quantity.
The actual values of attribute levels are strongly problem dependent. The settings differ profoundly among conjoint studies. The notion of the value psychologists call "just noticeable difference" is very useful. The difference between any consecutive attribute levels should be substantially larger.
An interaction between two attributes means that certain combination of some level of one attribute with some level of the other attribute is preferred noticeably more (or less) than is the average preference (the main effect) of the level of one attribute in combination with all other levels of the other attribute. For example, for the attributes "car type" and "car color", sport cars are more preferred in bright colors while luxury limousines in black.
Estimation of the interactions requires much more data than estimation of main effects. The total number of parameters to be estimated is one less than the product of the level numbers of the attributes involved in the interactions. It is usually much more than the effective number of degrees of freedom in the data that can be obtained in a conjoint exercise at a respondent level. Estimation is therefore feasible only at the sample or segment level. Interactions were useful before reliable methods for individual-based estimation of main effects have become available. Most of the then found interactions have been recognized as a numerical fit of the heterogeneity in the sample. In the trivial example above, an individual prefers either a sport car or a limousine, and in a limited number of color hues. The interaction is irrelevant.
The main problem in estimation of interactions is the one inherent to any of the main effects but in an enhanced way. If a profile with certain level is either never or always chosen, all the interactions related to the level are inestimable. An approach minimizing the interviewing and estimation costs is required. In some cases it is possible to modify the design by replacing the original attributes with attributes composed of combinations of their levels. Some unimportant combinations can be omitted and the number of the parameters to be estimated decreased. Values of main effects created this way are understood better than interactions, and their interpretation is simpler.
Estimation of interactions is reasonable provided the group of respondents is homogeneous in perceptions and induced behavior that reflect the interactions. This is hardly achievable in practice. In most cases known to us, validity of estimated interactions was questionable even when done for a carefully selected sample. An alternative approach is to group respondents in the first estimation pass according the latent classes identified in the data, and to estimate interactions for each group separately in the second estimation pass. There is a disadvantage in the ex-post definition and interpretation of the sample groups. Once the part-worth estimation is based on the groups, other ways of sample segmentation are influenced or, in the worst case, biased.
Packaging and its size play an important role in FMCG/CPG product category. The type of packaging is clearly a level of a nominal attribute. The size of package can be treated either as a simple quantity, usually bound to a price discount, or each size can be treated as a nominal level. As usual, it is important to imitate the real retail conditions. The actual design of the conjoint exercise depends on the size of choice-sets, the method of choice-set generation, and the prohibitions between the attributes involved in interactions of the packaging attribute levels.
As the total number of possible interactions between the products (brands) and package formats can be prohibitive, some simplification is unavoidable. The reduction is possible by grouping the similar products and their packaging formats into classes. The decrease in number of estimated parameters leads to a gain in reliability of the estimates.
Components of goods and services bundled into packages interact strongly and often quite unexpectedly. A proven solution is to create a composite attribute of product bundles or packages such that impossible or illogical combinations of components are eliminated. The number of parameters to be computed can be substantially reduced compared to the full interaction model. In addition, the transformation of interactions into main effects greatly simplifies interpretation.
A mistake would be to expect that adding an item to a package when leaving all other attributes intact (including e.g. the total price) will lead to a higher acceptance of the package. Quite too often the potential user is uninterested in the added item or suspects some additional expenses or difficulties might be related.
Optionally selectable items can be studied using the MBC - Menu Based Choice interviewing and estimation method. If the core product is complicated, or there are too many of them, or the task would be too difficult, it is wiser to interview the options in a separate exercise. Choices of options can be simulated conditionally given the choice of the base product.
Presence of interactions between levels of two attributes does not mean the attributes involved are correlated. The term correlation is reserved for the relationships between attribute levels in the design of the conjoint exercise. It has strong influence on reliability of estimated parameters but has nothing common with the behavioral aspects of respondents.
Choice-based experiments are, in general, more efficient in determining relative importances of product features than classic evaluation-based (metric) interviewing methods. However, pitfalls are not excluded. Time to time it is observed that respondents tend to ignore an attribute that is known as important in the real product. One can only guess the reason. It seems that less comprehensible attributes, e.g. those with long descriptions, are often omitted from consideration or simply misunderstood. If there are many attributes some of them may be neglected due to their position in the profile, say next to the most important attribute. Or the attribute may be known as being set on one of its level in all the currently marketed products, and either not believed to be changed or believed to be changed in all products in the same way by all suppliers in the future. Or the attribute is more susceptible to verbal or visual presentation such as those rendered in advertisements rather than thought important rationally. The reader may devise other causes.